前言
在我开始研究 foc 的时候,所有的书籍都在介绍 park 变换和 clarke 变换。有一种魔力告诉你,没这俩变换,就写不成 foc.
然而事实的真相并不是如此。
foc 要控制什么
首先得了解,在 foc 发明前,电机是如何控制的? foc 发明以前,无刷电机采取的是六步换向法。电机每旋转60度,控制器就要进行一次“电子换向”。控制器输出的,是同一时刻 只有2条线有输出的方波。
由此,在方波时代,电机控制器要控制的无非就是方波的电压。
真的是这样的吗?
事实上,经常玩航模的童鞋就知道。航模的电调,有一个参数叫“换向提前角”。电调会在本不是换向的时间提前换向。这个提前的时间点,从时间上来说自然是和转速有关。从角度上来说,就和转速无关了。所以叫提前角,而不是提前时间。
为何要提前换向呢?转子还没到该换向的位置,为何要提前换向呢?
如果这个问题没有搞明白,是无法理解 foc 的。
foc 之所以需要电流采样,本质上就是为了确定提前换向角。而不是像航模的电调那样还得人工配置。
为啥要提前换向呢?
因为磁场是电流建立的,不是电压建立的。而绕组是一个电感。电感的电流会滞后电压。准时换向,不过是让电压和转子呈 90度角度。而电流滞后,会导致电流并不和转子呈90度,也就是磁场没有和转子呈90度夹角,也就是扭矩没有最大化发挥。
要最大化发挥电机的扭矩,要磁场垂直于转子,电压就必须有一定的提前量。这个提前量,就只能通过对电流的采样获取。
所以, foc 的目的,就是让定子磁场垂直于转子磁场。而电流的采样,就是为了获得电流对电压的滞后角,从而对电压角进行提前。
前人为啥要进行 park/clark 变换
教材上说,是为了将三相变两相。因为两相少一个变量,好控制。
其实那都是教材不懂装懂瞎说的。三相电流本来就只有2个属性。幅值和相位。这个幅值,说的是他完整周期内的最大值。
但是,最大值,一个周期里只出现2次。也就是说,在某个采样的瞬间,你拿到的,大概率都只是中间的某个值。难道要连续采样一个完整周期才才能确定最大值吗?
不能。
那如何能在采样的瞬间,就能直接知晓最大值和相位呢?
前人的答案之一,就是 逆 clark 变换 + 逆 park 变换。
三相坐标系里的角度描述很困难
因为我们的数学工具,对角度的描述,是在平面直角坐标系里的。三相电,其实是在平面三维坐标系里的。如果你有数学工具可以直接在这种平面三维坐标系里工作,那就不需要进行变换。
但是,如果我们将这个变换,限定在一个模块呢? 只限定在电流采样模块。
电流采样模块,只对上层输出两个参数, 电流的交流幅值,和当前的相位角。
那么,整个电机的控制代码,就不会再有任何一个地方需要 park/clark 变换. 而且电流采样那边,只进行一次反clarke 变换。而这个反 clarke 变换,就只是三相瞬时电流转幅值+相角描述的一个转换。
那么整个电机控制流程逻辑,就会变得异常清晰明白。不会有反直觉的变换掺杂其中。
甚至,电流采样是 foc 达到最大效率的一个手段。没有电流采样,不过是效率不能最佳化。所以这个电流采样甚至不是初期必修课。
所以前人是为了自己软件工程上的考虑
前人是为自己软件实现方便上的考虑。既然电流采样这边是必须要进行变换。否则无法获得电流相角。那就索性其他地方也全部改成二维坐标系。 而前人的这个决定,被后人东施效颦,只敢模仿,不敢超越。
先抛开电流采样
如果不进行电流采样,foc 的算法如何控制呢?
算法的输入有2个: 期望的扭矩值,当前转子位置。 输出有3个: 分别是三个相位的 pwm 占空比。
当前的转子位置,推导出来的是 输出的电压相位值。方法是 转子位置+90度+提前角。 提前角暂取 0.
根据期望的扭矩值,推算出来的是 电压幅值。这个电压幅值+电压相位值,最终就变成了 三相电的各自电压值,然后得出 pwm 占空比。
那么三相电压各自的值,由电压幅值*sin(相位值) 获得。另外2相,依此落后120度。然后各自的值,和 直流母线电压的比值,就是 pwm 占空比。
这个是 spwm 法。其实还有个不同的算法,可以获得三相各自的 pwm 值。这个方法其实脱胎自无刷电机方波控制的六步换向法。
六步换向法实际上在驱动电机的时候,是在电压角为转子角度60度的时候,换一次向,于是电压提前转子120度。然后转子转60度后,再次换向。
也就是说,定子磁场的方向是固定的6个方向。 定子磁场和转子磁场夹角缩小到60度的时候进行换向。定子磁场和转子磁场角度就会在 120度和60度之间波动,阶梯前进。 (当然,这是在不考虑电流滞后效应的情况下。)
而 svpwm ,就是让磁场在 60度和120度之间来回切换,模拟出90度夹角。也就是,用6个固定的矢量,合成出一个360度无死角的矢量。这就是空间矢量合成名字的由来。
进行矢量合成,是用的临近的2个矢量合成的,所以进行了6个扇区的划分。这样就能知道该用哪两个矢量进行合成。
在进行合成矢量的时候,会计算出3个时间, T0 T1 和 T2 。 这三个时间,分别是 “无输出” , 输出 距离转子最近的矢量,和稍微远点的那个矢量。
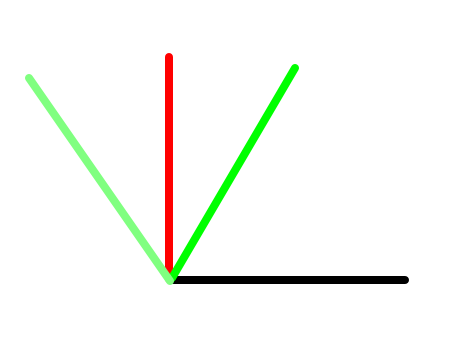
如图,黑色是转子的方向,红色是希望生成的定子磁场的方向,两个绿色就是本次要调用的2条矢量。 T1 是深绿色的矢量时间,T2 是浅绿色的矢量时间。
T1 和 T2 的时间之比,就决定了 红色这条合成的定子磁场方向。而 T0 时间,就决定了红色的长度。
而 T1 和 T2 的时间,其实很好算,就是 红色和两条绿色线里的两个夹角的 sin 值。
有了 T1 和 T2 时间,就该利用 红线所在的扇区,把矢量的时间分配,变成 mos 管的导通时间分配。
于是就有了各大 foc 算法里的那个长 switch case 语句
你看,在进行 svpwm 输出的时候,是不需要进行什么park变换的。就只需要考虑要输出多大幅值的交流电,要输出的相位角是多少。
决定提前角
在上面,红色是磁场方向。我们输出交流电的时候,是假定磁场方向和电压方向相同。 但是实际上,磁场方向会滞后。因为线圈有电感值,电流相位会落后电压。
但是,具体会落后多少,无法提前知道。只能实时测量。而且每次测量的时候,获得的只能是某个具体一瞬间的3个电流值。
比如,我测得 0.5A 0.5A -1A 三个电流值。那么如何知道,这个交流电的峰值? 因为这个峰值,是进行电流闭环控制所必须的数据。 而相位,也是进行计算提前角的必须数据。
三相交流电,其合成矢量,其实是绕着一个圆进行圆周运动。所以,其实是可以利用3矢量合成法。 就获得了最终的合成矢量。而这个合成矢量的长度,就是三相电电压的幅值。这个合成矢量的方向,就是三相电的相位角。
所以,其实这里既可以直接按矢量进行计算,也可以进行 Clark 变换后,变成2维坐标,再进行 park 变换后, 获得所谓的 q 轴 和 d 轴电流。 如果 PID 控制算法的作用目标是让 Id = 0, 则最终输出的电压 Vd, 经过 反 clarke 变换后,恰好就会让电压(相比于使用90度垂直)的提前角 = 电流的滞后角。
所以,既可以让 PID 算法去逼近 Id= 0 的目标,也可以算出电流相位滞后角后,直接对电压的相位角进行提前。
为何前人会选择让 PID 算法去逼近 Id = 0
因为park提出这个算法的时候,电机控制还属于新兴行业。并没有cpu这种东西可以用来奢侈的进行控制。
所以,电机输出用的 pwm 波,其实是用 纯电路,三角波和比较器输出的。 硬件电路,特别适合进行“负反馈”操作,对自己的输出进行锁定。
于是,他们设计了硬件的 park 变换电路,然后用硬件电路进行 负反馈。完成锁相角的任务。 已说到锁相角,搞模拟电路的让应该非常熟悉一个词, PLL。
后来把控制任务搬到软件上的时候,他们就沿用了这套控制流程。
而他们搬迁的时候写的 “电机库” 就被业内程序员奉为圭臬了。
Comments