轮子上的三条辐条
如果有一个轮子,半径为 1 ,在滚动的时候,其圆心会始终离地1高度。整个轮子的最顶端,也始终离地高度2.
如果在这个轮子上,画出三条辐条。辐条夹角 120度。
轮子在滚动的时候,辐条的顶部会完美的走过一个正弦波。波峰为 2. 中心为 1 。
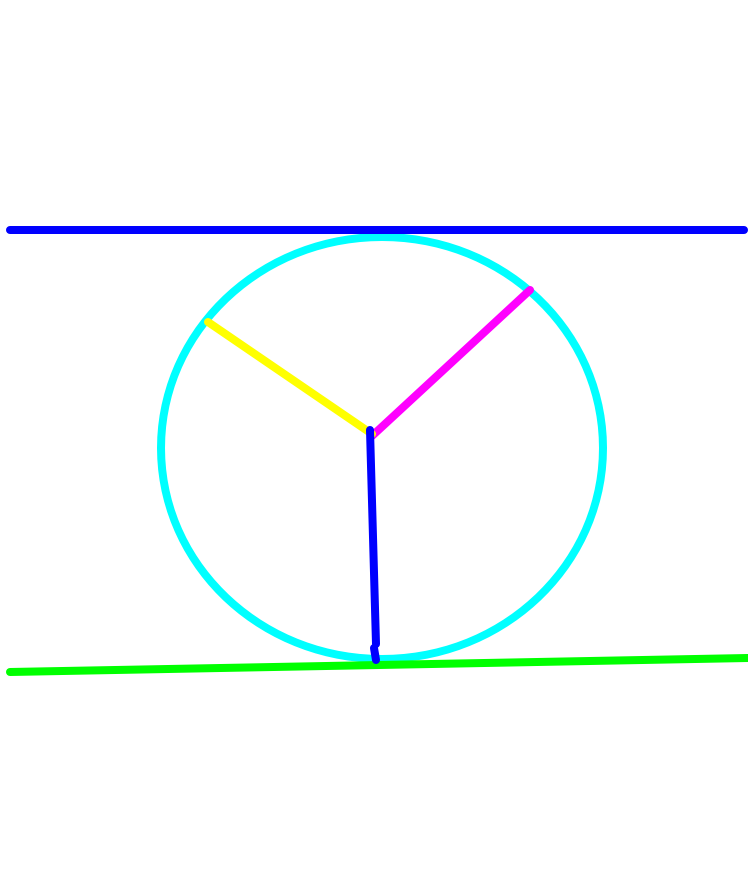
这,就是正选波调制的三相电。其相电压的幅值为1。线电压为 $\sqrt{3}$. 由于轮子最高处为2。 因此正弦波调制的直流电压利用率就是 $\sqrt{3}/2$
去掉轮毂,只留下辐条
因为没了轮毂,只留下辐条,于是,车轮前进的时候,辐条的端点划过的波,却不是正弦波了,而是一个马鞍波。
因为车轮的中心,在上下跳动!
于是,辐条的最高点,就不再是2了。因为车轮中心点最高的时候,恰恰两个辐条各自 120 分开。
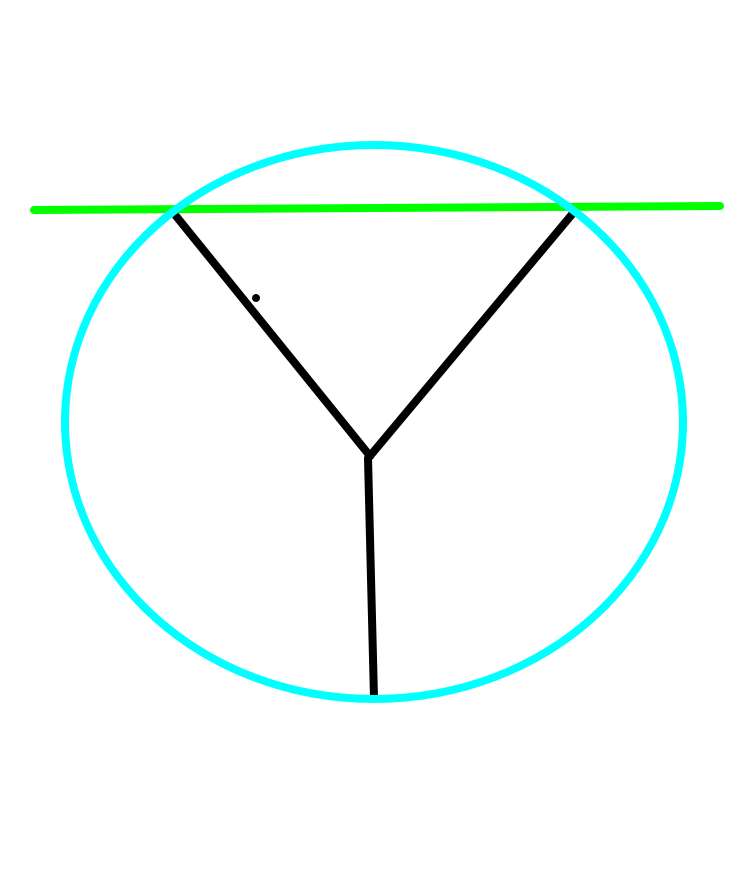
达不到2高度啊!
经过计算发现,其实车轮最大的高度,也只堪堪达到了 $\sqrt{3}$
这意味着,直流母线电压不需要为2 ,只需要 $\sqrt{3}$ 就能达到和之前一样的相电压输出!
于是,会发现,在这种马鞍调制下,直流母线电压的利用率达到了 100%。
虽然说,马鞍波的是各个相对 直流 地 的电压。
但是,相和相之间的电压波形,依旧是完美的正弦波。因为其马鞍波,实际上是正弦波上叠加的一个三次谐波。车轮中心的上下运动,恰好抵消了这个谐波。
于是相电压为完美的正弦波。而没有叠加的谐波。
Comments